
编者按
对于宽窄哲学的探讨,不仅仅是理论意义,而且具有迫切的必要性和珍贵的实用价值。在2018宽窄哲学高峰论坛上,专家学者铿锵发言,从不同层面、不同维度对宽窄哲学作出了深刻阐述,对宽窄哲学在应用和实践层面的发展和创新进行了探讨,进一步丰富和完善了宽窄哲学体系,诠释了大家对现实世界的不懈探索与思考精神。让我们跟随他们的哲思与心路一起来探究宽窄哲学的魅力,共同探讨宽窄哲学伟大力量!

四川成都武侯祠有一副对联:“能攻心则反侧自消,从古知兵非好战;不审势即宽严皆误,后来治蜀要深思”。在成都市中心还有一个著名的景点,叫“宽窄巷子”,每天游人如织,十分热闹。这对联和巷子正好说明,宽窄在心,宽窄在蜀,宽窄是认识问题、是辩证法,“宽窄学”诞生在成都。宽窄系统论是把宽、窄作为概念元素研究其内涵、外延、结构、层次、组合、演变、功能、应用的学科,包括宽窄维度观、变换观、曲面观、整体观、价值观、人生观,涉及宽窄量子论、超弦轮、控制论、突变论、信息论、混沌论、分形论、孤波论、复变论、耗散论、协同论、张量论、超循环论等领域,属于宽窄科技哲学。
第一是宽窄维度观
宽窄与空间维数有关,在不同维数时宽窄不同。宽窄不是客观存在,只是比较方式,与人的立场、观点、方法有关。不同的人,对宽窄的理解和认识不同。在不同的空间中,宽窄不同。宽窄是一种“量子纠缠”,有宽就有窄,有窄就有宽。从物理学来看,宽窄与空间维数、运动速度密切相关。维数越高越宽,维数越低越窄。人间冲突发生的根本原因是空间维数不够大。比如在二维是窄,在三维就是宽;在三维是窄,在四维就是宽。通常认为太窄,是因为空间维数较小。尤其是在现代非线性科学中,把整数维数(如1、2、3、4等)拓展到了分数维数(如1.3、2.6、3.5、4.2等),空间连续化,宽窄就大大延伸。这是分形(fractal)理论研究的课题。在高维空间里,宽窄随时可以变换。在量子力学中,物质具有波粒二象性,宽窄不定,这是“宽窄量子论”。在超弦理论中,基本粒子分割到极致时就是弦的振动,宽窄没准,这是“宽窄超弦论”。在可见光范围,可以看到宽窄,但在极长和极短波长区间就难于看到宽窄。在复数和张量空间,不能比较宽窄。在暗物质和反物质空间,不知宽窄。以光速(30万公里每秒)为参照,物体运动接近光速,时间进程会变慢,长度会变短,质量会变大。甚至认为,当速度超过光速就会时光倒流。在高维和强大引力情况下,时空可以折叠,比如北京到华盛顿的距离可以为零。空间折叠是一种因为强大的引力使空间发生扭曲的现象。这种现象是真实存在的,因而在理论上只要能达到一定的引力就能使空间发生弯曲,相当于要从一张平整的纸一端到另一端除了走两点间的直线外,还可以直接把纸叠起来,让两点靠近。因此人们普遍认为黑洞能够穿越遥远的空间,因为黑洞具有无比巨大的引力,连光都不可逃脱它的吸引,在这样的引力下空间也有极大的可能被折叠,这也就使得以不超越光速却能在短时间内进行宇宙旅行成为了可能。皮亚诺曲线(Peano curve)是一曲线序列的极限。只要恰当选择函数,画出一条连续的参数曲线,当参数t在0、1区间取值时,皮亚诺曲线将遍历单位正方形中所有的点,得到一条充满空间的曲线(图1), 皮亚诺曲线是一条连续而不可导的曲线,是分数维数。皮亚诺(Peano)曲线是一条能够填满正方形的曲线。在传统概念中,曲线的维数是1维,正方形是2维。

(图1:皮亚罗曲线)
第二是宽窄人生观
宽窄人生观是人们在社会空间实践中形成的对于人生目的和意义的根本看法,对待生活的态度。宽窄与心态有关。孔子曰:“三十而立,四十而不惑,五十而知天命,六十而耳顺,七十而从心所欲,不逾矩”(《为政》)。这里的“天命”就是“宽窄”,就是人生规律和社会规律。人生道路是越走越窄,还是越走越宽?不同的人答案不同。世界本无宽窄,宽窄全在心间。世上本无难易,难易全在感悟。可从宽窄见心态,看境界。地球是窄,宇宙是宽。小河是窄,大海是宽。固体是窄,气体是宽。吸烟是窄,吐烟是宽。个人是窄,集体是宽。回家是窄,上班是宽。私享是窄,共享是宽。地狱是窄,天堂是宽。死亡是窄,活着是宽。静止是窄,运动是宽。有限是窄,无限是宽。有形是窄,无形是宽。囚禁是窄,自由是宽。在山脚是窄,在山顶是宽。只顾自己是窄,心怀全球是宽。酒在杯中激荡是窄,烟在空中弥漫是宽。种子下到田间是窄,烟叶制成商品是宽。由宽走向窄是深度,由窄走向宽是大度。宽窄是认识论、辩证法、智慧学。上善若水任方圆。水有固态、液态、气态三种状态,宽窄尽展,但不能脱离地球,总有边界。记忆是窄,忘记是宽。人的许多痛苦源于比较和记忆,其实自由才是人生最高境界。平等、民主、幸福的前提是自由,失去自由就失去一切。人格、尊严、财产都将失去。因此,自由是最基本的需求,囚犯就是被剥夺自由。人的需求分为动物性、心理性、发展性、符号性、实现性、超越性等类别,但主要是生理性和社会性需求。调整心态就改变了宽窄。
第三是宽窄变换观
宽窄变换观是指空间尺度随着立场观点而变化,思想境界不同宽窄不同。1981年,西拔牙学者圣地亚哥·卡拉特拉瓦(Santiago Calatrava)凭借天才的论文《论空间结构的可折叠性》获得博士学位,这篇论文是他走向大师道路的起点。他提出了一个结构理论:试图系统地生成与示范将三维结构折叠成二维结构,再变为一维结构。这与电影《盗梦空间》中折叠城市空间一样奇妙,但他是由精确的计算与缜密的分析得出的结论。2016年3月3日,在美国911事件世贸大厦遗址上,新的世贸中心交通枢纽地铁车站开放了,它像一只展翅的白色钢铁巨鸟,这就是由西班牙建筑大师卡拉特拉瓦设计的。中国科幻小说《北京折叠》,讨论了一些经济学和社会学的问题,它提出空间是可以折叠的,大地是可以翻转的。拓扑学(topology)是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。在拓扑几何中,没有大小宽窄。它只考虑物体间的位置关系而不考虑它们的形状和大小。在拓扑学里,重要的拓扑性质包括连通性与紧致性。什么是拓扑呢?拓扑学被称为橡皮几何学。它们在图形被弯曲、拉大、缩小或任意的变形下保持不变,只要在变形过程中不使原来不同的点重合为同一个点,又不产生新点。换句话说,这种变换的条件是:在原来图形的点与变换了图形的点之间存在着一一对应的关系,并且邻近的点还是邻近的点。这样的变换叫做拓扑变换,两个图形叫同胚。同胚是两个拓扑空间之间的双连续函数。同胚是拓扑空间范畴中的同构。因为如果图形都是用橡皮做成的,就能把许多图形进行拓扑变换。例如,一个橡皮圈能变形成一个圆圈或一个正方形圈或三角形圈。但是一个橡皮圈不能由拓扑变换成为一个阿拉伯数字8。因为不把圈上的两个点重合在一起,圈就不会变成8。“莫比乌斯带”是一种拓扑图形(图2B),正好可以两点不重合,但能从里走到外,或从外走到内。这是在公元1858年,由德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁发现的:把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而莫比乌斯带这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘(也是说,它的曲面只有一个)。假如人类的身体可以像橡胶人一样任意变形,那么用两手的拇指和食指做成两个套着的圆环之后,我们可以不放开手指,把圆环给解开来(图2A)。
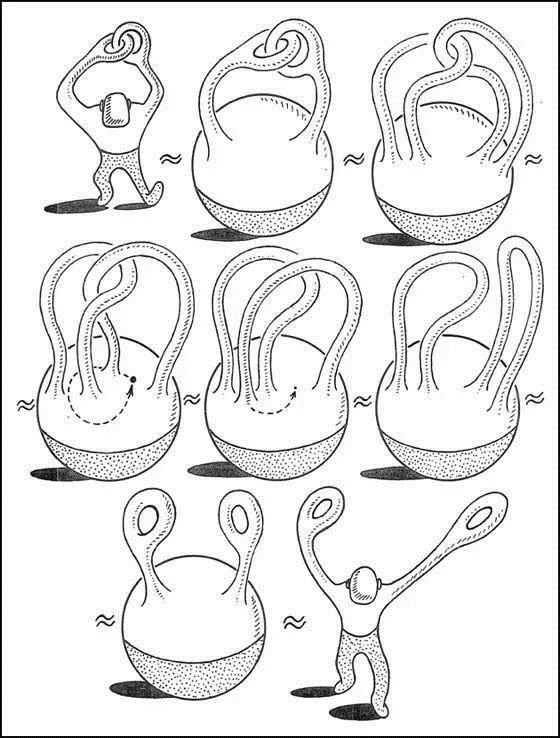
(图2A:橡皮人的拓扑变换)
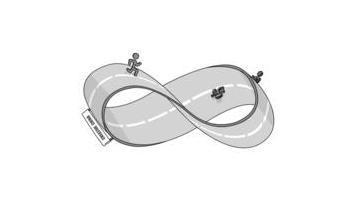
(图2B表示只有一个曲面的莫比乌斯带)
彭罗斯阶梯(Penrose stairs)是一个有名的几何学悖论,指的是一个始终向上或向下但却走不到头的阶梯(图3),可以被视为彭罗斯三角形的一个变体,在此阶梯上永远无法找到最高的一点或者最低的一点。彭罗斯阶梯由英国数学家罗杰·彭罗斯及其父亲遗传学家列昂尼德·彭罗斯于1958年提出。彭罗斯阶梯不可能在三维空间内存在,但只要放入更高阶的空间,彭罗斯阶梯就可以很容易地实现。如同莫比乌斯环、克莱因瓶。

(图3为彭罗斯阶梯)
第四是宽窄曲面观
宽窄曲面观是指宽窄概念只在传统欧氏几何里有意义,在非欧几何里不存在固定不变的宽窄。非欧几何一般是指罗巴切夫斯基几何(双曲几何)和黎曼的椭圆几何。它们与欧氏几何最主要的区别在于公理体系中采用了不同的平行定理。欧氏几何的平行公理是:过已知直线外一点,只有一条直线与已知直线平行。非欧几何把平行公理改变为:过已知直线外一点,至少有两条直线与已知直线平行(罗巴切夫斯基),或者是:过已知直线外一点,不存在一条直线与已知直线平行(黎曼)。这是三种不同几何体系的根本差异。欧氏几何的三角形的内角和等于180°,在罗巴契夫斯基几何中,三角形的内角和总是小于180°,而在黎曼几何中,三角形的内角和总是大于180°。黎曼几何学不承认平行线的存在,它的另一条公设讲:直线可以无限延长,但总的长度是有限的。黎曼几何的模型是一个经过适当“改进”的球面,三维欧氏空间以及四维闵柯夫斯基空间都是黎曼空间的特例。直观上看,欧氏空间是平直空间。而非欧几何空间是凹凸的空间。在小尺度范围内,我们所处的现实空间近似于平直的,欧氏几何的公理是适用的。但是在微尺度和宏尺度范围,欧氏几何就不再适用,非欧几何可以更好地描述非平直(非均匀)空间的各种现象。爱因斯坦的广义相对论就是建立弯曲时空的基础上的。在广义相对论中爱因斯坦放弃了关于时空均匀性的观念,他认为时空只是在充分小的空间里以一种近似性而均匀的,但是整个时空却是不均匀的。黎曼几何的核心是张量,它是向量(有方向)的推广。黎曼空间是一种矢量空间(有方向),它满足空间中存在度规张量,使临近两点的距离由正定二次型决定。 张量的严格定义是利用线性映射来描述的。标量可以看作是0阶张量,矢量可以看作1阶张量。张量中有许多特殊的形式, 比如对称张量、反对称张量等。欧式几何中的度量是零曲率的,而黎曼几何研究更一般的度量,在不同的度量下,空间的曲率是不同的。粗略地说,牛顿力学是建立在欧式空间上的,而广义相对论的时空是一个黎曼流形(Manifold)。流形,是局部具有欧氏空间性质的空间。一般的流形可以通过把许多平直的片折弯并粘连而成。
更为通俗的解释是,欧氏几何是把认识停留在平面上了,所研究的范围是绝对的平的问题,认为人生活在一个绝对平的世界里,因此最近有本书叫《世界是平的》,作者描述了当代世界发生的重大变化,展示了“全球化正在滑入扭曲飞行的原因和方式”,揭开这个世界的神秘面纱,深入浅出地讲述复杂的外交政策和经济问题。在平面里画出的三角形三条边都是直的。两点之间的距离也是直的。但是假如我们生活的空间是一个双曲面(不是双曲线),这个双曲面可以想象成一口平滑的锅或太阳罩,我们就在这个双曲面里画三角形,这个三角形的三边的任何点都绝对不能离开双曲面,我们将发现这个三角形的三边无论怎么画都不会是直线,那么这样的三角形就是罗巴切夫斯基三角形,经过论证发现,任何罗氏三角形的内角和都永远小于180度,无论怎么画都不能超出180度,但是当把这个双曲面渐渐展开时,一直舒展成绝对平的面,这时罗氏三角形就变成了欧氏三角形,其内角是180度。在平面上,两点间的最短距离是线段,但是在双曲面上,两点间的最短距离则是曲线,因为平面上的最短距离在平面上,那么曲面上的最短距离也只能在曲面上,而不能跑到曲面外抻直,故这个最短距离只能是曲线。若我们把双曲面舒展成平面以后,再继续朝平面的另一个方向变,则变成了椭圆面或圆面,这个时候,如果我们在这个椭圆面上画三角形,将发现,无论怎么画,这个三角形的内角和都大于180度,两点间的最短距离依然是曲线,这个几何就是黎曼几何。这个几何在物理上非常有用,因为光在空间上就是沿着曲线跑的,并非是直线,我们生活在地球上,因此我们的空间也是曲面,而不是平面,但为了生活方便,都不做严格规定,都近似地当成了平面。黎曼曲率α等于1、-1和0的空间分别是黎曼球空间、罗巴切夫斯基空间和欧氏空间。如图4。(下转P6)(上接P5)公式(2-7-6)表示非欧几何长度S与欧式几何长度X的关系。
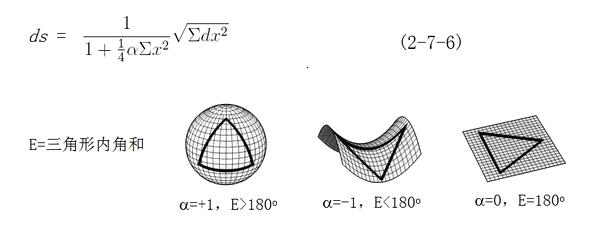
(图4表示三种几何概念)
爱因斯坦在1915年以几何语言建立而成的引力理论,将引力描述成因时空中的物质与能量而弯曲的时空,以取代传统对于引力是一种力的看法。他预见,物质的存在可能造成空间的弯曲。万有引力不是真正的力,而是时空弯曲的表现。广义相对论解释:地球并不受引力牵引,而是保持惯性运动,由于太阳的质量使空间弯曲,地球的弯曲轨道根本就是惯性运动轨道,是弯曲时空中的短程线(相当于平直时空的直线)。弯曲的空间没有直线,只有最短线,平直的空间里,直线即最短线。在广义相对论中,引力被描述为时空的一种几何属性(曲率),将引力解释成四维空间的曲率。而这种时空曲率与处于时空中的物质与辐射的能量-动量张量直接相联系,其联系方式即是爱因斯坦的引力场方程(一个二阶非线性偏微分方程组)。
第五是宽窄价值观
宽窄价值观是基于人对空间尺度的感悟而作出的认知、理解、判断或抉择,也就是人认定宽窄事物、辩定是非的一种思维或取向。宽窄价值观具有稳定性和持久性、历史性与选择性、主观性的特点,对动机有导向的作用。传统价值论在数学化程度上的局限性,从根本上决定了它在实际应用上的局限性。宽窄价值论的出现,冲破了传统研究思路的约束,实现了价值论的逻辑化、数学化、美学化、科学化、实效化,把主观与客观、有形与无形、精神与物质、需求与供给整合了起来,闯出了一条充满希望的新路子。宽窄不是对立统一,而是差异协同。椭圆哲学、协商民主、小我与大我、现在与未来、古代与现代,四川与世界、盆地与全球,都是协同关系,甚至是“量子纠缠”现象,可以创建“宽窄学”。这门学科属于认识论、方法论、世界观、价值观范畴,可以提升人品、人格、品质、品格,提高产品质量和层次。在宽窄价值论中,有十大定律:转化定律,就是宽窄可以互换;层级定律,就是宽窄有不同能序;互补定律,就是宽窄可以相互填充;协同定律,就是宽窄可以耦合促进;相对定律,就是在确定时空宽窄可以比较;取向定律,就是己所不欲勿施于人则由窄到宽;品位定律,就是高为宽低为窄;审美定律,就是眼宽物美心小路窄;连续定律,就是宽窄可在【0,1】中连续变化;感恩定律,宽是感恩窄是受惠,互予互动。
第六是宽窄整体论
宽窄整体论是指从全局考虑问题的观念,指自然界本身是一个有机大系统,人和其他的生物都是其中的一部分,如果这个整体或某一部分受到损害,那么其他方面也将受到影响和破坏。一切皆过程。宽窄是过程,是层级、是认识、是境界、是品味、是人格。在前面的宽窄研究中,我们已经提出宽窄相对论、价值论、模糊论、智慧学等。现在,应该进行总结,建立“宽窄系统论”和“宽窄学”,完善宽窄概念、范畴、原理和应用。宽窄系统论,是在宽窄视域下研究事物元素、组成、层次、结构、功能及其相互联系、作用的学说,是唯物辩证法及非线性系统论的认识论部分,本质是系统元素的耦合、协同、转化和升华。宽窄学,是研究宽窄内涵、外延、原理及应用的学科。系统论的基本思想是把研究的对象看作一个整体来对待,从整体出发来研究各要素的相互关系,从本质上阐明其结构、功能、行为和动态,从而把握整体达到最优的目标,产生新的质,1+1大于2,非线性效应,学科包括控制论、突变论、信息论、混沌学、分形学、孤波学、耗散结构、协同学、超循环等。在数学中,几何点没有大小、形态,因此抽象的元素没有大小和形态。元素有个数、状态和关系的区分。一个系统可以被定义为元素的集合和元素之间关系的总和。在宽窄学中,就是由不同宽窄尺度可以构成系统,宽窄是尺度谱系。
宽窄控制论。通过信息反馈调节,实现宽窄变化。1834年著名的法国物理学家安培写了一篇论述科学哲理的文章,他把管理国家的科学称为“控制论”,把希腊文译成法文“Cybernetigue”。1948 年诺伯特·维纳发表了著名的《控制论——关于在动物和机器中控制和通讯的科学》。维纳发明“控制论”这个词正是受了安培等人的启发。目前,控制论的思想和方法已经渗透到了几乎所有的自然科学和社会科学领域。维纳把控制论看作是一门研究动态系统在变的环境条件下如何保持平衡状态或稳定状态的科学。实际上,控制论是研究各类系统的控制、信息交换、反馈调节的科学,是跨及众多学科的交叉学科。控制的基础是信息,主要原理是反馈论,一切信息传递都是为了控制,进而任何控制又都有赖于信息反馈来实现。通俗地说,信息反馈是指由控制系统把信息输送出去,又把其作用结果返送回来,并对信息的再输出发生影响,起到制约的作用,以达到预定的目的。要求有一个预定的稳定状态或平衡状态;从外部环境到系统内部有一种信息的传递;这种系统具有一种专门设计用来校正行动的装置;这种系统为了在不断变化的环境中维持自身的稳定,内部都具有自动调节的机制,换言之,控制系统都是一种动态系统。因此,与那些只研究特定的物态系统,揭示某一领域具体规律的专门科学相比较,控制论是一门带有普遍性的横断科学。在控制论中,实施迭代运算,因此大小、宽窄可以调整改变。
宽窄突变论。通过量变与质变实现宽窄变化。控制论是研究自然界和人类社会中连续渐变如何引起突变或飞跃,并力求以统一的数学模型来描述,预测并控制这些突变或飞跃的一门学科。它把人们关于质变的经验总结成数学模型,表明质量既可通过飞跃的方式,也可通过渐变的方式来实现,并给出了两种质变方式的判别方法。控制论表明,在一定情况下,只要改变控制条件,一个飞跃过程可以转化为渐变,而一个渐变过程又可转化为飞跃。突变论认为事物结构的稳定性是突变论的基础,事物的不同质态从根本上说就是一些具有稳定性的状态,这就是为什么有的事物不变,有的渐变,有的则突变的内在原因。在严格控制条件的情况下,如果质变经历的中间过渡状态是不稳定的,它就是一个飞跃过程; 如果中间状态是稳定的,它就是一个渐变过程。在突变过程中,宽窄也变化了!另外,在自然和社会界,存在“自组织临界现象”(S0C),就是通常说的“最后一根稻草压死骆驼”,比如地震、社会动乱等,就是能量积累到极限或临界状态就会突变。
宽窄信息论。通过信息反馈调控宽窄关系。信息是与物质、能量同等重要的概念。信息是确定性的增加。本质上,信息论是运用概率论与数理统计的方法研究信息、信息熵、通信系统、数据传输、密码学、数据压缩等问题的应用数学学科。通常将克劳德·香农(Claude Shannon)于1948年10月发表于《贝尔系统技术学报》上的论文《A Mathematical Theory of Communication》(通信的数学理论)作为现代信息论研究的开端,香农被称为“信息论之父”。信息论将信息的传递作为一种统计现象来考虑,信息传输和信息压缩是信息论研究中的两大领域。这两个方面又由信息传输定理、信源-信道隔离定理相互联系。信息论中熵的概念与物理学中的热力学熵有着紧密的联系。互信息(Mutual Information)是指两个事件集合之间的相关性。把宽窄定义为两个事件X和Y,其互信息为:
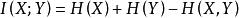
其中是联合熵(Joint Entropy),其定义为:

香农给出了信息熵的定义:
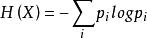
这一定义可以用来推算传递经二进制编码后的原信息所需的信道带宽。熵度量的是消息中所含的信息量。系统越复杂熵越大,越简单熵越小。不确定性越大,熵越大。熵增过程是一个自发的由有序向无序发展的过程。统计学定义:熵衡量系统的无序性。熵增是宽,负熵是窄。熵越高的系统就越难精确描述其微观状态。
宽窄混沌论。通过非线性作用改变宽窄状态。在科学上,如果一个系统的演变过程对初态非常敏感,就称它为混沌(Chaos)系统。“蝴蝶效应”就是典型的混沌现象。研究发现,混沌运动是由系统内部的非线性因素引起的。混沌学的基本观点是积累效应和度,即事物总处在平衡状态下的观点。混沌不是偶然的、个别的事件,而是普遍存在于宇宙间各种的宏观及微观系统的现象,万事万物,莫不混沌。如混沌气象学、混沌经济学、混沌数学等。混沌学不仅极具理论价值,而且能直接或间接创造财富。1975年,费根鲍姆研究周期倍增分岔发生时的参数之间的差率是一个常数,就是,若αn代表周期2的n次方的分支点(引起分岔时的α临界值),则(相邻倍化分岔点间的距离比)是一个常数:
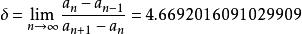
这是一个关于分岔宽窄变化的重要参数。此外,他发现 2n 周期分岔的超稳定点之间的距离 wn /wn+1之比也趋于一个常数 α, 称为费根鲍姆第二常数α=2.5029……。这些常数类似于圆周率π=3.14159…… ,自然对数底e=2.71828……一样重要。
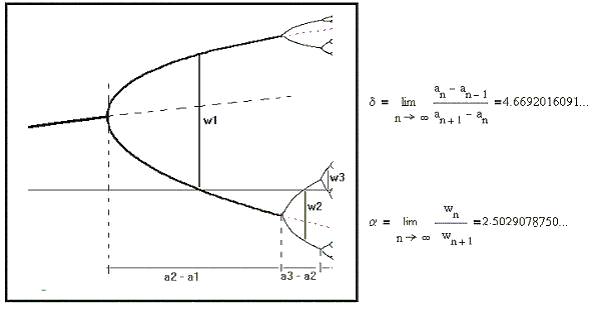
(图5:分岔与费根鲍姆常数)
宽窄分形论。通过自相似性改变宽窄概念。分形几何学(Fractal Geometry )是研究事物具有自相似性特征的数学。自相似就是局部形态与整体形态相似,具有无穷层次结构。简单地说,分形就是研究无限复杂具备自相似结构的几何学,是大自然复杂表面下的内在数学秩序。相对于传统几何学的研究对象为整数维数,如,零维的点、一维的线、二维的面、三维的立体乃至四维的时空。分形几何学的研究对象为非负实数维数,如0.63、1.58、2.72、log2/log3等。因为它的研究对象普遍存在于自然界中,因此分形几何学又被称为“大自然的几何学”。一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统。分形有几种类型,可以分别依据表现出的精确自相似性、半自相似性和统计自相似性来定义。适当地放大或缩小事物的几何尺寸,整个结构并不改变。虽然分形是一个数学构造,但同样存在自然界中(图6任何部分放大都相似,这是分形特点)。自然界的准晶体(一种介于晶体和非晶体之间的固体结,2011年诺贝尔奖),具有五次对称性,满足数学上黄金分割率0.618和斐波拉契级数特性,是分形的自相似结构。谢尔宾斯基三角形(Sierpinski triangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出。它是自相似集的例子,它的豪斯多夫维是log(3)/log(2) ≈ 1.585。 分形就是无限自相似,没有大小、宽窄。
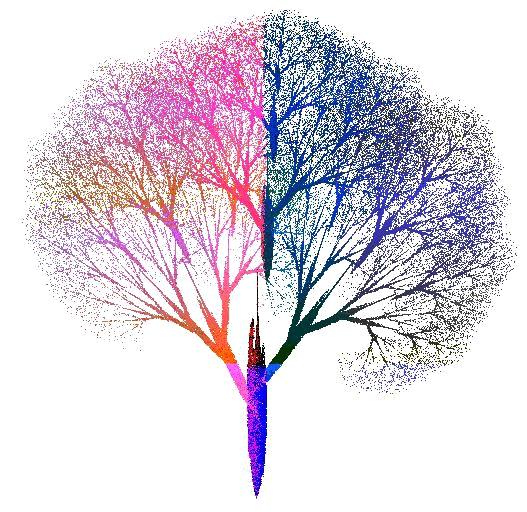
(图6A:分形树)

(图6B:分形的谢尔宾斯基三角形 )

(图6表示分形的自相似)
宽窄复数论。复数不能比较大小。没有大小就没有宽窄。宽窄分布与黎曼Zeta函数(复数)有关。复数z=a+bi(a,b为实数),其中i2= -1为虚数单位,即i来表示-1的平方根。当b=0时,z为实数,可以比较大小;当b不为零时,z为虚数,(a=0时为纯虚数),不能比较大小,只能比较“模”大小。向量(矢量)是既有长度又有方向的量,向量的模可以比较大小,但因为向量有方向,所以不能比较大小。因此在研究向量时,既要研究向量长度,又要研究向量的方向,方向没有大小之分,不能比较两个向量的大小。张量具有典型性,可以建立“宽窄张量论”。张量是有长短和多个方向的量,不能简单比较大小。张量是一组有序的数,每个数称为这个张量的分量。在坐标变换时,这些数按照一定的规则同时改变。比如在三维空间,零阶张量又称标量,由一个数组成,在任何坐标系下都相等,如物体的质量;一阶张量又称矢量,有三个分量,在不同的坐标系下,各个分量的值不同,但实际都是同一个矢量;二阶张量有9个分量,常用的有应力张量、应变张量等。在自然数序列中,质数就是那些只能被1和自身整除的整数,比如2,3,5,7,11等等都是质数,4,6,8,9等等都不是质数。由于每个自然数都可以唯一地分解成有限个质数的乘积,因此在某种程度上,质数构成了自然数体系的基石,就好比原子是物质世界的基础一样。非常大的质数目前被用于密码系统。虽然数学家对质数研究已久,但目前来看,质数在数轴上的出现似乎是随机而无规律的。最近关于黎曼定理的证明和质数定理、Zeta函数的报道,说明质数并不是完全随性而为,它的表现始终臣服在黎曼Zeta函数零点的分布规律上。Zeta函数是关于s的函数,其具体的定义就是自然数n的负s次方,对n从1到无穷求和(图7)。因此,黎曼Zeta函数就是一个无穷级数的求和。然而,遗憾的是,当且仅当复数s的实部大于1时,这个无穷级数的求和才能收敛(收敛在这里指级数的加和总数小于无穷)。为了研究Zeta函数的性质,黎曼通过围道积分的方式对该函数做了一个解析延拓,将s存在的空间拓展为复数平面,于是就有了黎曼猜想。零点就是那些使得函数的取值为零的数值集合(相当于方程的“根”集合)。比如一元二次方程一般有两个零点,并且有相应的求根公式给出零点的具体表达式。黎曼对解析延拓后的Zeta函数证明了其具有两类零点。其中一类是某个三角sin函数的周期零点,这被称为平凡零点;另一类是Zeta函数自身的零点,被称为非平凡零点。针对非平凡零点,黎曼提出了三个命题。第一个命题,黎曼指出了非平凡零点的个数,且十分肯定其分布在实部大于0但是小于1的带状区域上。第二个命题,黎曼提出所有非平凡零点都几乎全部位于实部等于1/2的直线上。第三个命题,黎曼用十分谨慎的语气写到:很可能所有非平凡零点都全部位于实部等于1/2的直线上。这条线,从此被称为临界线。而最后这个命题,就是让后世数学家如痴如醉且寝食难安的黎曼猜想。因此,破译黎曼猜想就等于完全确定了质数跳舞的规律和秩序。新发现将有助于数论、密码学和材料科学的研究。美国普林斯顿大学研究人员发表于Journal of Statistical Mechanics: Theory and Experiment的一篇论文指出,准晶体内部原子排列位置与质数序列存在联系。通过X射线对材料的分析可高精度预测质数。与典型晶体相比,准晶体的布拉格峰排列更为复杂和独特,准晶体布拉格峰之间,仍存在较小布拉格峰,发现质数也存在自相似组,即在某些高度的峰值之间存在较小峰值的组。许多复杂分形也是复数函数,如朱利亚集(JuliaSet)是一个在复平面上形成分形的点的集合。

(图7:黎曼及Zeta函数)
宽窄孤波论。通过相干性实现宽窄变化。无穷多自由度是宽,有限流体物质是窄。孤波(Soliton wave,又称孤子波、孤立子、孤立波)是一类由于非线性作用引起的横波,它在运动过程中形状保持不变,是非线性科学三大前沿之一,应用于物理、数学等诸多领域。孤波的特点是具有定域性、稳定性和完整性,平时很难找到一种直观的图像。钱塘江大潮可能是一种孤波。现代物理学认为,孤子是一种相干结构,主要存在于具有无穷多自由度的连续介质或流体复杂系统中。在相干结构中有无穷多个守恒的物理量。在水中的孤波要保持其形状,就其“内部”来说必须有能量势差,从而推动水分子在水堆内部运动,同时通过能量(按守恒定律)交换的方式维持这种能量势差。如果我们将能量势差的中值点记为零,那么水堆就是依靠正能量势差和负能量势差维持其形态的。孤波解是一类特殊的非线性偏微分方程的行波解。
宽窄耗散论。通过自组织实现宽窄变化。耗散论是研究系统耗散结构的性质及其形成、稳定和演变规律的科学。它着重阐明开放系统如何从无序走向有序的过程。有序是窄,无序是宽。一个远离平衡态的开放系统通过不断地与外界交换物质和能量,在外界条件变化达到一定阈值时,可以通过内部的作用产生自组织现象,使系统从原来的无序状态自发地转变为时空上和功能上的宏观有序状态,形成新的、稳定的有序结构。这种非平衡态下的新的有序结构就是耗散结构。耗散论提出“非平衡是有序之源”的观点。但非平衡,不是不平衡,也不是平衡,而是巨涨落前的远离平衡态,是处于失稳临界点附近没有超过临界点的稳态。现代医学强调的是动态平衡。要使机体完成“无序→有序”的跃进,必须使机体远离平衡即机体要有相当的自身活力和抵抗力,通过涨落达到临界点才能使新的跃进完成,使机体从无序状态恢复到有序状态。耗散结构理论的创始人是伊里亚·普里戈金(Ilya Prigogine)教授,他在1945年得出了最小熵产生原理,由于对建立耗散结构理论方面的贡献,荣获了1977年诺贝尔化学奖。
宽窄协同论。通过协同耦合改变宽窄。协同学(Synergetics )由德国物理学家赫尔曼·哈肯在20世纪70年代初提出,它是研究各种由大量子系统组成的系统在一定条件下,通过子系统间的协同作用,在宏观上呈有序状态,形成具有一定功能的自组织结构机理的学科。它以信息论、控制论、突变论等一些现代科学理论为基础,吸取平衡相变理论中序参量的概念和绝热消去原理,通过对不同学科领域中的同类现象的类比,进一步揭示了各种系统和现象中从无序到有序转变的共同规律。同耗散结构理论一样,协同学的研究对象也是远离平衡态的开放系统,但它进一步指出系统从无序到有序转化的关键并不在于系统是平衡或非平衡,或是偏离平衡状态的远近,而在于组成系统的各个子系统之间的协同作用,就是说,不仅处于非平衡态的开放系统,而且处于平衡态的开放系统,在一定的条件下,都可呈现出宏观的有序结构。序参量可能就是主变量,是决定性因素。
宽窄超循环论。宽窄无限可分,无限循环,可以转化,可以协同耦合,可以复制再生。这是超循环论(The Hypercycle)的思想。这个理论是由德国科学家艾根(Manfred Eigen)于1970年提出的。艾根认为生命信息的超源是一个采取超循环形式的分子自组织过程,他把生物化学中的循环现象分为不同的层次:第一个层次是转化反应循环,在整体上它是个自我再生过程;第二个层次称为催化反应循环,在整体上它是个自我复制过程;第三个层次就是所谓的超循环。超循环是指催化循环在功能上循环耦合联系起来的循环,即催化超循环。实际上在超循环组织中,并不要求所有组元都起着自催化剂的作用,一般地说,只要此循环中有一个环节是自复制单元,此循环就能表现出超循环的特征。超循环的特征就是:不仅能自我再生,自我复制,而且还能自我选择,自我优化,从而向更高的有序状态进化。超循环结构演化的内部因素主要来自两个方面:首先是自复制单元在复制过程中出现的差错,类似于基因突变;其次,超循环结构是由多组元耦合成的多层次系统,内部存在复杂的非线性相互作用,内在随机性在很大程度上起作用,它给超循环结构施加了另一个内扰动。由此可见,超循环结构的演化,大体上与三个因素有关:复制误差,内在随机性和环境扰动。超循环结构存在,进化必需满足三个前提条件:⑴以足够大的负熵流推动结构的新陈代谢;⑵以足够强的复制能力使系统信息得以积累遗传;⑶以组元间足够强的功能耦合保证结构的存在和发展。必须同时具备这三个条件,超循环结构才能稳定存在,发展进化,否则,退化是不可避免的。
总之,只要空间是柔性的或者是曲面的或者是高维的或者是分数的,宽窄就是不确定的。只要在高速的或者在强引力的或者在超弦的或者是在复数的情况下,宽窄就没有定数。在张量空间、暗物质空间和反物质空间,宽窄不能比较。宽窄看似普通平凡,其实充满玄机妙算;宽窄看似客观存在,其实就是虚实变换;宽窄看似近在眼前,其实处于明暗空间;宽窄看似简单初浅,其实属于科技前沿;宽窄看似几何形态,本质却是人性心态;宽窄看似天天相见,实际正是时时流变。宽窄系统学和宽窄学,是辩证法、是认识论、是世界观、是大智慧、是大概念、是大学问!
(本文作者系四川省社会科学院党委书记、教授李后强)











