人类是在不断的质疑中获得进步的，而每一次问题的发现，都会给人们的生活带来巨大的改变。而这样的情况，在各行各业中都有所体现，比如数学领域便是如此。数学是一片充满了理性的世界，也是一片充满了抽象性的世界，因此令普通人感到非常晦涩难懂。

　　但是不可否认的是，数学上的进步，能够给人们带来巨大的帮助。而这，便是人们研究数学的意义。在数学领域中，一共出现过三次数学危机，而今天本文讨论的重点便是第二次数学危机。倘若说起第二次数学危机，就不得不提到一个人，此人名为芝诺，生于意大利半岛南部的埃利亚城邦，他是埃利亚学派的著名哲学家巴门尼德（Parmenides）的学生和朋友。

　　芝诺曾经提出了一系列关于运动的不可分性的哲学悖论，他说：“运动是不可能的。由于运动的物体在到达目的地前必须到达其半路上的点，若假设空间无限可分则有限距离包括无穷多点，于是运动的物体会在有限时间内经过无限多点。”为了验证自己的说法，芝诺还举了三个例子：第一、“阿基里斯追不上乌龟”。

　　他提出让乌龟和阿基里斯赛跑，乌龟在阿基里斯前面1000米处开始跑，并且假定阿基里斯的速度是乌龟的10倍。当比赛开始后，若阿基里斯跑了1000米，设所用的时间为t，此时乌龟便领先他100米；当阿基里斯跑完下一个100米时，他所用的时间为t/10，乌龟仍然前于他10米；当阿基里斯跑完下一个10米时，他所用的时间为t/100，乌龟仍然前于他1米……

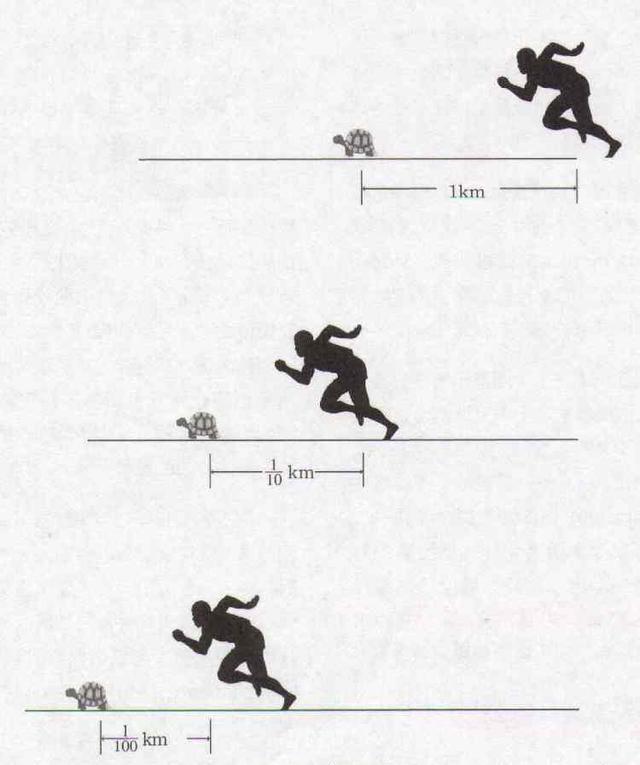
　　芝诺认为，阿基里斯能够继续逼近乌龟，但绝不可能追上它，因为阿基里斯总是首先必须到达乌龟的出发点，因而乌龟必定总是跑在前头。这个论点同两分法悖论一样，所不同的是，不必把所需通过的路程一再平分。第二，“飞矢不动”。意思是箭在运动过程中的任一瞬时间必在一确定位置上，因而是静止的，所以箭就不能处于运动状态。但由于箭要达到每一时刻的固定位置必须存在动能，所以箭必须是运动状态。

　　这个悖论的问题在于，“飞行”的运动，是依赖于两个时间点的。即从这一刻到那一刻的时间内，这支箭是否移动。另外，中国古代的名家惠施也提出过，“飞鸟之景，未尝动也”的类似说法。第三，“操场或游行队伍”。

　　A、B两件物体以等速向相反方向运动。从静止的c来看，比如说A、B都在1小时内移动了2公里，可是从A看来，则B在1小时内就移动了4公里。运动是矛盾的，所以运动是不可能的。前两个悖论诘难了关于时间和空间无限可分，因而运动是连续的观点，后两个悖论诘难了时间和空间不能无限可分，因而运动是间断的观点。说明了希腊人已经看到“无穷小”与“很小很小”的矛盾，但他们无法解决这些矛盾。其后果是，希腊几何证明中从此就排除了无穷小。

　　既然问题产生了，就需要解决，因此在后面很长的一段时间内，人们都陷入了不断的思考之中，并最终在17世纪晚期，形成了无穷小演算——微积分这门学科。牛顿和莱布尼兹被公认为微积分的奠基者，他们的功绩主要在于：把各种有关问题的解法统一成微分法和积分法；有明确的计算步骤；微分法和积分法互为逆运算。由于运算的完整性和应用的广泛性，微积分成为当时解决问题的重要工具。

　　参考资料：《芝诺悖论》、《趣味数学》