作者:大神团·张通
作者介绍:张通,新东方智慧学堂授课老师,北京大学力学系理论与应用力学专业学士。
石头剪刀布,这个游戏相信大家都玩过,比赛一局肯定是运气做主,但是多次对局,则是一个策略游戏。那么问题来了,两人重复多次石头剪刀布的对局,且两人都绝对“聪明”,那么是否存在一种最优策略,使得胜率最高?

游戏,又叫博弈。研究游戏的学科,在数学中叫博弈论Game Theory。本文不用去管博弈论的定义,只需要知道什么情况下的游戏可以用博弈论来解决。
就是说,石头剪刀布这个游戏必须满足以下几个特点:
1、参与游戏的主体完全理性。
最大化自己的收益,即能赢绝不输,能多赚绝不少赚。若参与游戏的主体是两个人,各自仅代表自己为战,这种博弈可称为“双人博弈”。
2、完全理性是共同认识。
即两个人都知道对方是理性的,也知道对方知道我是理性的,也知道对方知道我知道对方是理性的……直到无穷。
3、参与者每局都有自己的策略选择权及收益信息且能做出正确选择。
比如能出石头、剪刀或布中的任意一个,且知道规则:石头战胜剪刀战胜布战胜石头,如果知道对方出布,自己一定出剪刀。
从上面三点可以看出,石头剪刀布均满足,所以该问题可称石头剪刀布博弈问题。
博弈论的种类很多。
第一,如果游戏状态信息(包括双方的偏好、策略、游戏规则、双方的收益信息)对双方完全可见,则称完全信息博弈;反之,只要有任一个信息对任一方不可见,则称不完全信息博弈。
第二,游戏是两个人同时(包括逻辑同时,即一方行动后另一方完全不知,等同于同时行动)决策并行动,则称静态博弈;反之,决策一先一后,就像下棋一样,则称动态博弈。
第三,游戏中有有限个参与者且每位参与者的策略选择只有有限种,则称有限博弈;反之,则称无限博弈。


本文研究的问题均为完全信息静态有限双人博弈,石头剪刀布博弈正是其中的一种。但它的策略选择较为复杂,故先看一些简单的例子。
著名的“囚徒困境”是博弈论中最经典也是最简单的例子。
问题描述如下:两个罪犯,被警察分别关在两个独立的不能互通信息的牢房里进行审讯。他俩都可以做出自己的选择:供出另一个人,或保持沉默。这两个罪犯都知道,如果他俩都能保持沉默,均会只被判一个月;但如果有一个人先供出他的同伙,那么这个人就可以被无罪释放,但被他供出来的那个会被判十八个月;如果他俩都招供了,则两个人都会被判十二个月。
如果你是罪犯,你会如何行动?
本文研究的这类博弈的策略和收益信息是完全公开的,故可以用收益矩阵来表示。即:

表头第一列是A的行动策略,第一行是B的行动策略,表中的数字分别表示在该组合行动下的A的收益和B的收益。
对A来说,若B供出同伙,则A供出同伙比沉默要少判六个月,所以A选供出同伙;若B沉默,则A供出同伙比沉默要少判一个月,所以A选供出同伙。于是尽管A不知道B做何种选择,但他知道无论B选择什么,他选择供出同伙总是最优的。显然,根据对称性,B也会选择供出同伙。
于是最终的结果是两人均供出同伙,最后均会被判十二个月。而这个结果也被称为“均衡”,(跟物理学中的“稳定”类似)即在“均衡”时,任一方都没有动力改变当前策略,从而都维持“均衡”的稳定性。
比如,双沉默就不是“均衡”,因为A有动力从当前的“沉默”改为“供出同伙”,从而收益增加。

从结果来看,即使两个人都绝对“聪明”,但并没有选择全局最优(总判刑时长最短)的策略——双沉默。这个情况在当今普遍存在,个体的利益和集体的利益很多时候都是冲突的,想要解决这个矛盾,一般需要第三方来促成合作。如果不存在第三方,还有一种可能,通过重复博弈来促成合作。
假设重复n次,注意到最后一次博弈一定是双招供,同时前n-1次博弈的结果不会对最后一次的决策产生影响,则倒数第二次博弈,同理也是双招供,递推回到第一次博弈,一直都是双招供。
结论:该博弈是“非零和博弈”,有唯一的纯策略均衡,但和全局最优不同。可以通过第三方介入达到“双赢”,但重复博弈和单次博弈并没有区别。

那就要问了,什么情况下重复博弈能促成合作呢?接下来看一个类似的问题——无规则交通博弈。
在无任何交通规则下开车迎面遇到一辆车,你可以通过向左偏移或向右偏移来避开车,对方完全相同,此时如何选择?

因为两车顺利通过对双方都有利,而撞车对双方都不利,所以收益可以定性化,即记两车顺利通过的收益为1,撞车的收益为-1。收益矩阵如下:

易知均向左偏与均向右偏都是均衡。
由于事先没有规则和沟通,所以实际博弈时,无法得到确定性的结果。但我们又为了得到(或避免)这种均衡,有时候还需要找到一个混合策略(有别于纯策略,是指每种策略选择均赋予对应的概率,纯策略也是一种特殊的混合策略,即看成是该策略赋予1的概率,而其他策略均赋予0的概率)均衡,即均以 的概率向左偏或向右偏。
很明显均向左偏与均向右偏都是全局最优,但一次博弈很难实现这个局面,试想,如果两人都要面对这种选择很多次,则双方均有动力在第一次行动时,试探性地选择混合策略来促成合作,一旦出现均向左偏或均向右偏的局面,则之后永远选择这种局面即可,另一方面在第一次的混合策略中,有 的概率未达到均衡,第二次继续该混合策略,仍有 的概率未达到均衡,未达到均衡的概率呈等比数列减小趋于零,只需继续下去,总会出现前述均衡的局面。
结论:该博弈是“非零和博弈”,有多于一个纯策略均衡。可以通过第三方介入,或重复博弈来达到“双赢”。

接下来看看文初的石头剪刀布,很明显这是一个“零和博弈”。
同样,因为对双方来说,胜利收益大于平局收益大于失败收益,所以收益同样可以定性化,记胜利收益为1,平局收益为0,失败收益为-1。
收益矩阵如下:

逐个检验所有可能知,该博弈没有纯策略。
这点是比较显然的,任何一方要避免自己的选择带有规律性,因为一旦自己的选择有某种规律性并被对手发现,则对手可以根据这种规律预先猜到你的选择,从而针对性地选择战胜你。比如你出石头的概率多于其他两个,则对方一旦发现,就多出布;你总是石头—剪刀—布循环出,则对方就布—石头—剪刀;你赢了就换,输就不换,则对手赢了和输了都不换,等等。
因此双方在博弈过程中,必须随机选择策略,或者说,最优的策略就是将自己当成一台抽签机器,出石头、剪刀、布的概率均为 。在这个混合策略下,双方的胜率均为 ,期望均为0。
这个结果是符合常识的,甚至不用博弈论也能得到答案。

继续考虑下面这个游戏。还是石头剪刀布,双方在同一起跑线上开始,如果一方赢了,且赢的一方是出石头就走10米,出剪刀就走2米,出布就走5 米。最后比谁走得更远。问最优策略和每局的期望。
同样先写出收益矩阵:

注意到,以上所有收益矩阵,单独看A和B是完全一样的,所以不难得出双方策略完全一致的结论。逐个检验所有可能知,该博弈仍没有纯策略。于是考虑混合策略,不妨设B出石头、剪刀、布的概率分别为 ,于是有 。
跟上一个问题一样,要保证两个原则:
第一,不能让对方知道自己的选择,必须利用随机性。
第二,每种策略的概率一定要恰好使对方无机可乘,即让对方无法通过针对性地倾向莫一策略而有优势。
于是得到结论,B的概率分布要使得A的三种策略收益相同(否则A就会选择收益大的那个策略,由于这是一个零和博弈,对方收益大就意味着自己收益受损,所以B有动力重新调整自己的概率分布),均衡的策略是满足 (A出石头的收益等于出剪刀的等于出布的)。
解得 、 、 ,同理B的策略一样。
结论:最优策略为AB均采用 的概率出石头、 的概率出剪刀、 的概率出布,每局的期望是 米。
通过上述博弈问题发现,找最优策略就是找均衡,因为最优策略一定是均衡的,而均衡就是双方利益的平衡点。
那么问题又来了,如果没有均衡怎么办?
这个问题在1950年由著名数学家、经济学家约翰·纳什John Nash证明,该定理叙述如下:每一个有限博弈必存在至少一个混合策略均衡。故均衡通常也称为纳什均衡,纳什也因为在均衡分析理论中的贡献而获得了1994年的诺贝尔经济学奖。著名电影《美丽心灵》主角的原型就是约翰·纳什。

该证明需要用到角谷静夫不动点定理,这里就不做详细证明了。
总结一下,拿到这类问题,首先写出收益矩阵,逐一检验所有可能找纯策略均衡。在找混合策略均衡时,先赋予每种策略概率,其概率分布使得对方的所有策略收益均相同,从而解出对应的概率,同理可求出另一方的。最后,每方概率分布下的混合策略组合就是该博弈下自己的最优策略。
到此石头剪刀布博弈问题完美解决了。这样的问题还有很多,但只要是完全信息静态有限双人博弈,就都可以用收益矩阵和策略均衡分析来解决。

最后留给大家一道练习题——约会博弈。
AB两人准备周末一起去看电影或者逛街,但事先未沟通去哪,已知A喜欢看电影,B喜欢逛街。若一起看电影A、B的收益分别为2、1;若一起逛街A、B的收益分别为1、3;若错过,双方收益均为0。问双方的最优策略和期望。
想一想,这道题应该怎么解?
(点击空白处查看内容)
▼
同样先写出收益矩阵:
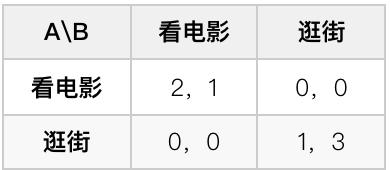
注意到,A和B各自的收益矩阵不再一样了,所以双方策略可能不一样。易知该博弈有两个纯策略均衡:一起看电影或一起逛街。同无交通规则博弈,由于事先没有沟通,所以无法得出确定性的结果于是考虑混合策略。不妨设A看电影的概率为 ,逛街的概率为 ,B看电影的概率为 ,逛街的概率为 ,于是有 (B看电影的收益等于逛街的收益); (A看电影的收益等于逛街的收益). 解得 、 。即A采用 的概率看电影、 的概率逛街,期望为 ;B采用 的概率看电影、 的概率逛街,期望为 。
来源:新东方智慧学堂
编辑:aloysius
来源:中科院物理所











